En esta entrada se estudiará el movimiento parabólico, que no es otro que el que describen los objetos que son lanzados en presencia de un campo gravitatorio uniforme (igual en todos los puntos del espacio) siempre y cuando se desprecie el efecto del rozamiento. En otras palabras, cualquier proyectil que sea lanzado en la Tierra o en cualquier otro planeta, si se desprecia la oposición que ejerce el aire en su desplazamiento, describirá una parábola.
El movimiento parabólico se puede entender como la composición (la suma) de dos movimientos:
- Un movimiento rectilíneo uniforme horizontal.
- Un movimiento rectilíneo uniformemente acelerado (debido a la gravedad) vertical.
El siguiente gif presenta la trayectoria que sigue un proyectil que es lanzado a una velocidad de 10m/s con una inclinación de 45º en un planeta ficticio cuya gravedad vale 2.5m/s2 (en la superficie de la Tierra vale aproximadamente 9.8m/s2).
Podemos observar cómo en dicho planeta el proyectil llegaría a una distancia de 40 metros.
Volviendo a la teoría, para definir la trayectoria de un proyectil es necesario definir:
- La posición desde la que se lanza (el punto (0,0) en el ejemplo anterior).
- La velocidad (módulo) con que es lanzado.
- La inclinación con que se lanza.
- La aceleración (gravedad) a la que es sometido.
En el siguiente applet se pueden variar todos estos parámetros para ver cómo cambia la trayectoria del proyectil. Una vez escogidos los valores se debe desplazar el deslizador del tiempo (seleccionándolo y presionando la flecha izquierda del teclado).
Si nos fijamos en las velocidades del proyectil (flechas azules) en cada instante de tiempo, podemos comprobar que la velocidad horizontal es siempre la misma, mientras que la vertical varía a lo largo del tiempo (debido al efecto de la gravedad). El momento en que la velocidad vertical se hace nula coincide con la máxima altura que alcanza el proyectil.
La velocidad total del objeto se obtiene sumando (vectorialmente) la velocidad horizontal y la vertical.
Otro hecho a tener en cuenta es que la velocidad total del objeto se da cuando alcanza el punto más alto, debido a que en dicho punto únicamente posee velocidad horizontal, mientras que en cualquier otro instante a la velocidad horizontal se le suma la velocidad vertical correspondiente. Por tanto el proyectil va perdiendo velocidad desde que es lanzado hasta que alcanza el máximo de altura y tras esto comienza a ganar velocidad progresivamente hasta que cae sobre la superficie.
La velocidad total del objeto se obtiene sumando (vectorialmente) la velocidad horizontal y la vertical.
Otro hecho a tener en cuenta es que la velocidad total del objeto se da cuando alcanza el punto más alto, debido a que en dicho punto únicamente posee velocidad horizontal, mientras que en cualquier otro instante a la velocidad horizontal se le suma la velocidad vertical correspondiente. Por tanto el proyectil va perdiendo velocidad desde que es lanzado hasta que alcanza el máximo de altura y tras esto comienza a ganar velocidad progresivamente hasta que cae sobre la superficie.
- Curiosidades
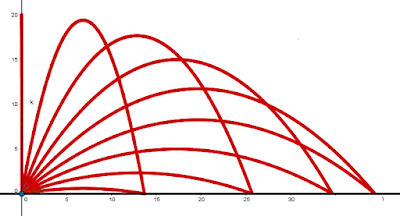
¿Cuál es la inclinación para la cual el proyectil llega a mayor distancia? Veamos qué ocurre cuando fijamos la posición del lanzamiento, la velocidad y la aceleración, pero vamos variando la inclinación del lanzamiento:
Así es, la respuesta es 45º. Por tanto, en las pruebas de lanzamiento de balon medicinal si consigues lanzarlo a 45º respecto del suelo tendrás mucho ganado.
Y ¿cuál es la inclinación para la cual el proyectil alcanza la mayor altura? En la siguiente imagen se ve el resultado de variar progresivamente la inclinación de lanzamiento, desde los 10º hasta los 90º.
Efectivamente, cuanto mayor es la inclinación mayor es la altura que se alcanza y la mayor altura se logra cuando se lanza el objeto verticalmente.
Otra pregunta, ¿qué ocurre si lanzas un proyectil con la misma velocidad e inclinación pero lo haces en diferentes planetas del Sistema Solar? Hay que tener en cuenta que cada planeta posee una aceleración de la gravedad distinta, en algunos casos es mayor que la de la Tierra (en Jupiter por ejemplo) y en otros casos menor (como en Marte o Saturno):